Let's try and get 1,000,000 replies to this post

I set my alarm for 5:45 so I could get up for the F1 qualifying but I couldn't find a stream in English so I'll just watch the highlight on the BBC later on. ::)
 
Forostar said:
Fits perfectly in the image of someone who voiced his opinions on the EU.
Click to expand...
Are you accusing me of racism Foro? :eek: Anyway, my Spanish isn't great and it would just have annoyed me not knowing what they're saying. Obviously a car driving around a racetrack is the same in any language and I can read the timings easily enough but if someone is talking I like to understand what they're saying. Although I just realized I could have muted my laptop and turned the radio on. ::):censored:
 
BW or anyone else, would you know how to solve this?

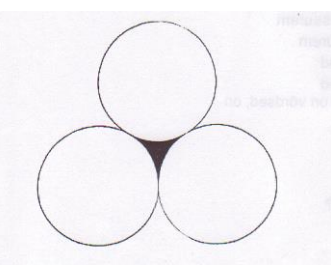
06688e31cf84f33324ca00a7a393cc31.png


The radius of one circle is 4 units. Find the area of the coloured section.
The answer, rounded, is 2,6 square units but I don't know how to get there. The area of one circle should be 16 pi square units so the area of all three is 48 pi square units. The circumference of one is 8 pi units. Where do I go from there?
 
I knew there had to be a triangle somewhere. The final equation is: 16 times square root of 3 - 8 times pi = (rounded) 2,6 square units.
16 times square root of 3 is the area of the triangle, which I understand, but how do you know that you have to subtract 8 times pi?
Thanks for the hint.
 
I needed Wingman's hint about drawing the triangle first. :innocent:

But yeah, area of one circle = 16*pi. Calculate the area of the triangle using 0.5*base*height where height is calculated with Pythagoras' Theorem so the area = 16*sqrt(3). The triangle contains the shaded area and a sector from each circle. The triangle is equilateral so each angle is 60º. As you realized the area of each sector will therefore be one sixth of the area of one circle, so area of a sector = (8/3)*pi. Since there are three of them the shaded area can be calculated by subtracting three times the area of a sector from the area of the triangle: 16*sqrt(3) - 8*pi = 2.58.
 
You must log in or register to reply here.
Back
Top